Technique photo : Nature de la lumière

FORMATION ET DEVELOPPEMENT DE L’IMAGE PHOTOGRAPHIQUE

Auteur Pierre Glafkidès
Physique et chimie photographique

• Caractère ondulatoire de la lumière
• Structure de la lumière
• Le photon
• L’onde électromagnétique
• Théorie de l’annihilation des photons
• Emission de rayonnement par la matière
• Action du rayonnement sur les atomes
• Effet photo-électrique
• Absorption de lumière par les molécules
• Emission stimulée de lumière. Lasers

Lire le post sur la lumière et la photochimie

Caractère ondulatoire de la lumière.

La lumière se propage en un mouvement vibratoire ou ondes.

Cette idée, émise par Huyghens au 17ème siècle, fut reprise par Young au début du 19ème siècle, puis développée successivement par Fresnel et Maxwell. Mais, entre temps, et à la suite des travaux d’Oersted et d’Ampère, Faraday développa la notion de champ, c’est-à-dire d’action par contact, représentée par des lignes de force à l’intérieur d’un diélectrique. Il découvrit, d’autre part, qu’un champ magnétique fait tourner le plan de polarisation d’un faisceau lumineux, laissant supposer, par là, une parenté étroite entre la lumière et le magnétisme.

Les expériences de Faraday formulées mathématiquement, d’abord par Gauss, furent mises à profit par Maxwell qui montra que les actions électromagnétiques se produisaient à la vitesse de la lumière. Précisant alors l’idée d’onde transversale, Maxwell considéra la lumière comme une perturbation électromagnétique. L’onde lumineuse est figurée, en chaque point de sa sphère d’émission, par deux vecteurs oscillants perpendiculaires, inscrits dans un plan lui-même perpendiculaire à la direction de propagation : l’un des vecteurs est électrique et l’autre magnétique. Un rayonnement est donc considéré comme
une variation périodique, dans l’espace, d’un champ électrique et d’un champ magnétique combinés.

Un rayon lumineux se propageant à une vitesse « c » accomplit, chaque seconde, un nombre d’oscillations complètes : v = c/λ. « v » est la fréquence de l’onde ; elle est d’autant plus élevée que « λ » est petit ( voir note 1). Comme oscillations durent une seconde, une seule oscillation dure un temps ou période : T=1/v seconde.

A la suite de Hertz qui, par des décharges oscillantes entre deux électrodes, montra que les ondes lumineuses et les ondes électriques ont une nature commune, on a pu représenter l’échelle des ondes électromagnétiques, sans discontinuité depuis les oscillations radioélectriques se mesurant par milliers de mètres, jusqu’aux rayons « λ » du radium inférieurs au 1/1 000 d’Angström :

• Ondes radioélectriques plusieurs dizaines de km jusqu’à 1 mm
• Radiations infrarouges (ou calorifiques) 1 000 µ à 0,74 µ
• Spectre visible 740 nm à 400 nm (ou mµ)
• Ultraviolet 400 nm à 10 nm (ou mµ)
• Rayons non définis 100 Å à 20 Å
• Rayons X mous vers 12 Å
• Rayons X durs vers 0,05 Å
• Rayons y du radium vers 0,001 Å

Tout rayonnement transporte de l’énergie. Cette énergie est décelable par l’œil humain (dans d’étroites limites) et plus généralement par la plaque photographique, la cellule photoélectrique, la pile thermoélectrique, le bolomètre (variation de résistance d’un ruban métallique) et le radiomètre de Crookes. On peut déceler ainsi un flux énergétique de 10-9 à 10-15 watt.

Note 1 : La longueur d’onde λ est caractéristique de la couleur (également sa fréquence « v », ce qui revient au même). La longueur d’onde se mesure en prenant pour unité le micron µ. (ou millième de millimètre), le nanomètre nm (millionième de mm ou millimicron mµ) et l’Angström Å (ou dix millionième de mm). 1 nm vaut donc 10 Å.

Structure de la lumière.

D’après la théorie ondulatoire, l’onde sphérique émise par une source lumineuse devrait se perdre dans l’espace par une dissémination progressive. Or il n’en est rien puisque, même après avoir parcouru des distances considérables, un rayon de lumière est capable de produire des effets photochimiques et photoélectriques qui nécessitent une certaine énergie.

La lumière est constituée de grains qui ne peuvent être fractionnés. Nous connaissons déjà la discontinuité de la matière qui se résout en fragments entiers indépendants : molécules, atomes, électrons… Une nature également discontinue de la lumière ne peut donc nous surprendre. Cette hypothèse, autrefois soutenue par Newton, fut reprise avec succès par Einstein.

Pourtant un rayon peut contourner un obstacle, comme le prouvent les phénomènes de diffraction et d’interférences, ce que ne saurait faire un projectile (qui serait entièrement dévié de son chemin).

Le caractère ondulatoire de la lumière étant un fait indiscutable mais insuffisant, il fallait trouver une explication rationnelle. Cela fut réalisé par l’ingénieuse association des deux théories corpusculaire et ondulatoire, d’ailleurs envisagée par Newton lui-même.

La mécanique ondulatoire, développée par L. de Broglie et Schriidinger, repose sur la théorie des quanta de Planck, perfectionnée par Bohr.

Cette théorie, suppose que les mouvements corpusculaires se font suivant une suite discontinue de valeurs entières, ou quanta.

La lumière, étant de nature vibratoire, n’est pas divisible à l’infini. Chaque oscillation complète correspond à une quantité d’énergie invariable h égale à 6,62.10-27 erg/s (voir note 2). « h » est la constante de Planck.

Si « v » est la fréquence de la radiation considérée (nombre d’oscillations par seconde) la quantité d’énergie mise en jeu pendant une seconde est « hv », dont la valeur est d’autant plus élevée que la longueur d’onde est plus courte. Par convention, on appelle « hv » quantum d’énergie ou photon.

Note 2 :  Erg : travail accompli par une force de 1 dyne déplaçant son point d’application de 1 cm dans la direction de la force. La dyne, ou 10-5 Newton, est la force qui, appliquée à une masse de 1 gramme lui communique une accélération de 1 cm par seconde F = my. 1 kg/mètre = 10′ ergs environ et 1 W = 107 ergs/s.

Le photon

Le photon est un corpuscule électriquement neutre, de masse presque nulle Il ne peut acquérir de l’énergie que grâce à sa vitesse très élevée.

La théorie des quanta, appliquée aux champs électromagnétiques, avait supposé, pour le photon, une masse nulle, afin d’être en accord avec les équations de Maxwell. Les calculs de la mécanique ondulatoire exigent, par contre, une masse non nulle, bien qu’extrêmement petite. Si la masse de l’électron est m = 0,9.10^{-27 g,}  Celle du photon ɣ serait de l’ordre de 10^-45 à 10^-65. Il en résulte que la vitesse de la lumière est une vitesse limite que le photon n’atteint jamais.

En étudiant l’électron, on s’aperçoit qu’il présente un spin ou moment angulaire de rotation (sur lui-même), accompagné d’un effet magnétique.

La quantité de mouvement du spin est mesurée en unité h/2π. Celui de l’électron a une valeur 1/2(h/2π) ; on dit que l’électron a un spin 1/2. Celui-ci ne peut prendre d’ailleurs que deux valeurs opposées : + 1/2 et — 1/2 suivant le sens de rotation.

Le photon est aussi doué de spin, mais égal à 1. Or le spin est la résultante de trois composantes rectangulaires. Le photon peut donc passer par différents états suivant les valeurs de ces composantes. L’une d’elles peut être positive, nulle ou négative, c’est-à-dire égale à +h/2π, 0 ou —h/2π. Si la composante est positive, il se forme un champ électrique et un champ magnétique perpendiculaires, qui accompagnent le photon. Le plan, formé par les directions de ces deux champs, est animé d’un mouvement de rotation vers la gauche, autour du troisième axe, celui de propagation. La vitesse angulaire de rotation est 2πv. Cette image correspond à celle de la représentation maxwellienne. Elle est analogue quand la composante du spin, suivant l’axe de propagation, est négative, sauf que le plan des champs électromagnétiques tourne à droite. On dit que la polarisation circulaire de l’onde est gauche ou droite. La combinaison d’une onde circulaire droite avec une onde circulaire gauche produit une onde polarisée rectiligne ou elliptique, suivant l’équivalence des deux ondes élémentaires ou la prédominance de l’une d’elles.

Dans le cas d’une composante de spin nulle, le photon se trouve accompagné seulement d’une onde électrique se déplaçant dans le même sens que lui.

Le photon de spin 1 est donc bien conforme au résultat des équations de Maxwell sur les ondes électromagnétiques. Cependant d’autres types d’équations mettent en jeu un photon de spin 0, encore inconnu.

On peut même considérer les photons de spin 1 ou 0 comme résultant de la fusion de deux corpuscules de spin 1/2 dont les spins s’ajoutent ou s’annulent. Ces corpuscules hypo­thétiques, l’ergon et l’antiergon, ont fait l’objet de maintes suppositions. On a pensé qu’ils seraient associés de la même manière qu’un électron avec un positon. En effet, un photon d’énergie supérieure à un million d’électrons-volts est susceptible de se matérialiser sous forme d’un positon et d’un électron, quand il traverse un atome. Inversement on peut dématérialiser le couple positon-électron sous forme de deux photons d’un demi million d’électrons-volts chacun. C’est le passage réversible de la lumière à la substance.

Les associations de photons suivent la loi statistique de Bose-Einstein, pour laquelle le même état peut appartenir à un nombre quelconque de corpuscules. Les électrons, au contraire, suivent la loi statistique de Fermi-Dirac où un corpuscule est seul à avoir un état particulier, à l’exclusion de tout autre corpuscule. Ce dernier principe, formulé par Pauli, pose que deux électrons ne peuvent suivre exactement la même orbite.

En résumé, la lumière est constituée de corpuscules d’énergie, ou photons, transportant une onde électromagnétique anisotrope.

L’onde électromagnétique

En fait, l’onde elle-même, qui caractérise l’état vibratoire du photon ne transporte pas d’énergie. L’onde n’a pas d’existence physique. C’est une fonction de probabilités, de fréquence déterminée, qui définit les positions du corpuscule dans le temps. On dit que le photon est piloté par une onde de probabilités.

La fonction d’onde e Ψ (x,y, z, t) du photon, appelée champ, a pour base une fonction de Lagrange, avec seize composantes mais on y fait intervenir un terme opérateur linéaire H (dit « hamiltonien et hermitien »). L’évolution de la fonction d’onde c.1, dans le temps, s’écrit alors :

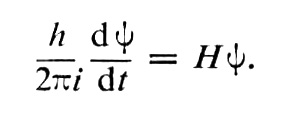
Comme il y a 16 composantes, on obtient 16 équations aux dérivées partielles simultanées. Ψ est donc une grandeur complexe formée de e Ψ1 e Ψ2 e Ψ3 etc. En substituant aux seize composantes primitives d’autres grandeurs d’un caractère particulier, on arrive à représenter les potentiels et les champs de la théorie électromagnétique classique.

Considérons maintenant un nombre n de photons dans les divers états énergétiques possibles. Leur évolution dans l’espace suit une fonction de répartition R telle que la probabilité pour qu’à l’instant t il y ait ni corpuscules dans l’état 1, n2 corpuscules à l’état 2, etc, soit donnée par [R(ni, n2, …, t)]². Cette fonction de répartition évolue suivant une équation du même type que celle indiquée pour Ψ mais où interviennent des opérateurs H sur les variables n. La théorie des quanta, appliquée aux champs électromagnétiques, assimile les grandeurs électromagnétiques, dépendant de l’espace

Théorie de l’annihilation des photons

L. de Broglie a développé une théorie suivant laquelle les photons peuvent « exister » dans un état particulier d’annihilation (représenté par une fonction d’onde 4(o) qui les rend inobservables. Pour disparaître ainsi, les photons doivent céder leur énergie et leur quantité de mouvement à des éléments matériels tels que des électrons ; c’est ce qui arrive pour tout photon absorbé par la matière. Inversement, sous l’influence de charges électriques, le champ électromagnétique qui se trouvait annulé se manifeste de nouveau et le photon redevient observable.
L’espace que nous appelons vide, serait alors peut être le réservoir d’un nombre immense et constant de photons annihilés, dont le champ est évidemment nul.

Mais les photons peuvent être inobservables sans être annihilés : par exemple les photons échangés par deux électrons voisins.
La théorie de l’annihilation permet d’expliquer l’existence du champ électrostatique entre deux électrons, la création par ces derniers d’un champ électromagnétique et l’émission de rayonnements par la matière.

Pour introduire la fonction de l’état annihilé Ψ(o) en mécanique ondulatoire il est nécessaire d’admettre que la propagation se fait non dans un espace à quatre dimensions (x_o, y, z, t) mais dans un espace à cinq dimensions (x_o, x, y, z, t) dans lequel x_o échappe à notre perception. Les composantes de la fonction Ψ de l’état normal du photon dépendent de x_o par le facteur e^ikoxo qui, introduit dans l’équation, donne pour les états non annihilés

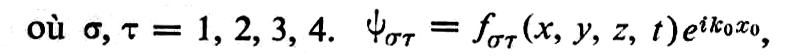
Emission de rayonnement par la matière

Considérons un atome en état de repos (ou stationnaire) : chaque électron parcourt l’orbite la plus petite qu’il lui est possible d’adopter, à condition que la longueur de sa trajectoire soit un nombre entier de fois la longueur d’onde associée. Dans cet état stable, d’énergie minimum, l’atome n’émet aucun rayonnement.
Si, pour une cause quelconque, un électron « saute » de l’orbite minimum à une orbite de rang supérieur, avec absorption d’une « quantité finie » d’énergie, l’atome se trouve alors dans un état activé, analogue à celui d’un ressort tendu. L’énergie potentielle de l’atome est augmentée.

Il peut arriver que le ressort se détende, nous voulons dire que l’électron activé retombe soit sur son orbite primitive, soit sur une orbite intermédiaire, avec diminution de son activation. Le surplus d’énergie que l’électron avait acquis se trouve naturellement libéré sous forme de rayonnement. Comme la plus petite particule d’énergie théorique est h (1 oscillation), et que l’énergie du photon est hv, la fréquence est égale au quotient de l’énergie perdue E par h : y = E/h.

Lorsque l’énergie libérée est suffisamment faible, l’émission lumineuse a lieu à proximité du spectre visible. Cette émission est le résultat de l’activation des niveaux périphériques seulement, plus faciles à perturber. C’est ce qui arrive avec les substances incandescentes usuelles.

Un mode particulier d’activation des atomes consiste à les bombarder, dans le vide poussé, par les rayons cathodiques (formés eux-mêmes par des jets d’électrons de vitesses variables). L’élément activé (ou anticathode) émet en se désactivant un rayonnement de fréquence très élevée : les rayons X. On constate que le spectre de ces rayons X varie avec chaque élément et le caractérise. Ce spectre est formé de groupes de raies correspondant aux divers niveaux énergétiques des électrons, que l’on peut ainsi repérer et étudier. Il devient alors possible, à l’aide des spectres de rayons X, de déterminer la structure électronique des éléments.

L’énergie perdue par un électron E_n – E_m: est approximativement liée aux caractéristiques de celui-ci par la formule

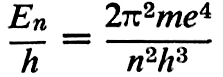
dans laquelle m est la masse de l’électron, e sa charge, h la constante de Planck, n un nombre entier positif. E_n/h a reçu le nom de terme spectral. Le dédoublement des raies d’émission de l’hydrogène a conduit Sommerfeld à une formule plus complète, généralisée par Rydberg :

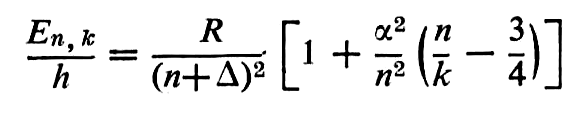
où X est la « constante de structure fine », n et k des nombres entiers, et ∆ une quantité caractéristique pour chaque élément.
En réalité, une raie de lumière émise par un corps est constituée de plus de deux raies très rapprochées. Se basant sur les propriétés du spin, Dirac a fait dépendre les termes spectraux de trois « nombres quantiques » n, l et j. Pour qu’il y ait émission à une certaine fréquence, il faut que la probabilité de transition de l’électron d’un état à un autre ne soit pas nulle.

Dans le cas des corps radioactifs, le rayonnement y (photons à très haute fréquence) est dû à l’altération du noyau par départ d’hélions (noyaux d’hélium). Les corpuscules constituant le noyau lourd du corps radioactif sont répartis sur des niveaux d’énergie, comme le sont les électrons planétaires. Tout départ d’un hélion provoque une redistribution des niveaux énergétiques avec activation, et désactivation accompagnée d’émission de photons.

Action du rayonnement sur les atomes

Un photon qui rencontre un atome peut perturber le mouvement et l’état d’un électron, par action électromagnétique. Si l’énergie de ce photon ne correspond à aucun état d’excitation dans l’atome, il est réémis dans une autre direction : il y a diffusion. La diffusion est d’autant plus importante que la fréquence est plus élevée.
Si l’énergie du photon correspond à un niveau d’excitation dans l’atome, le photon disparaît, après avoir cédé son énergie. On dit qu’il y a absorption. La fréquence du photon absorbé correspond à celle des photons qu’on peut émettre.

Un électron perturbé peut sauter sur une orbite plus éloignée, si l’énergie du photon concorde avec celle du niveau considéré (résonance). Plus la différence des énergies est grande, plus les probabilités d’arrachement diminuent.
Les électrons activés peuvent cependant retomber sur leur orbite primitive ou sur des orbites intermédiaires successives jusqu’à atteindre cette dernière, avec émission chaque fois d’un rayonnement de plus faible énergie, donc de plus grande longueur d’onde.

Dans l’action des rayons X sur les atomes, la longueur d’onde des photons absorbés est constante et caractéristique pour chaque niveau d’électrons (spectres de rayons X).

Effet photo-électrique

Quand les photons provoquent l’arrachement complet d’un électron périphérique, celui-ci s’échappe de l’atome, créant ainsi un courant électrique : c’est l’effet photoélectrique. Les photons s’annihilent en cédant leur énergie :

hv = travail d’excitation + énergie cinétique emportée par l’électron.

L’énergie nécessaire à l’arrachement correspond à l’énergie d’ionisation de l’atome, qui est de 4,3 eV pour le potassium, par exemple.

C’est ainsi qu’un rayon lumineux fait jaillir d’une mince pellicule de métal alcalin (potassium ou césium) déposée au fond d’une ampoule remplie d’un gaz inerte sous pression réduite, un nombre d’électrons proportionnel au nombre de photons reçus, c’est-à-dire proportionnel à l’intensité lumineuse. Le faible courant électrique obtenu est amplifié avant d’être utilisé.

Il peut arriver que l’énergie des photons ne corresponde pas aux états d’excitations des électrons de l’atome. Si la fréquence du rayonnement incident est élevée (rayons X, y) il est possible d’avoir à la fois diffusion de photons et éjection d’électrons : effet Compton.

Absorption de lumière par les molécules

Toute lumière qui traverse une substance, sort appauvrie d’un certain nombre de photons de longueurs d’ondes déterminées : il y a absorption sélective. Cette absorption est constante et caractéristique de la substance considérée. Si les radiations absorbées sont situées en dehors du spectre visible, elle nous paraît incolore. Si certaines radiations visibles sont absorbées, elle paraît colorée par les rayons transmis ou réfléchis. Enfin si la majeure partie des radiations visibles est absorbée, la substance est noire ou d’apparence foncée.

L’absorption, dans les régions allant de l’ultraviolet à l’infrarouge, dépend de la constitution moléculaire. Or les molécules sont le siège de trois sortes de mouvements (donc de variations d’énergie) :

• Mouvement de rotation des molécules mêmes autour d’un axe perpendiculaire à l’axe de liaison principal des atomes.
• Mouvement de vibration des noyaux
• Mouvement des électrons et notamment des électrons périphériques.

Chacun de ces mouvements provoque des absorptions de photons. Les très grandes longueurs d’onde de l’infrarouge (10 à 100 p.) correspondent généralement aux rotations moléculaires. Celles de 1 à 10 p., aux mouvements vibratoires. Toutefois certaines vibrations peuvent provoquer des raies fines d’absorption dans l’ultraviolet. Mais les radiations voisines de la région visible du spectre, proche infrarouge à ultraviolet, correspondent à un état électronique de la molécule, et qui se manifeste par un système de bandes d’absorption.

Cet état électronique dépend non seulement de la nature et du nombre des atomes en présence dans la molécule, mais aussi des distances relatives de leurs noyaux et de leurs positions. Il dépend donc des orbites parcourues par les électrons périphériques du système associé, et de leurs divers états énergétiques. Pour qu’il y ait absorption il faut qu’il y ait résonance entre l’état vibratoire des photons incidents et celui du système électronique de la molécule.

Emission stimulée de lumière. Lasers

Un atome peut acquérir un état excité qui lui permet, par retour à l’état normal, d’émettre un rayonnement. Mais la lumière émise par ces désexcitations spontanées est incohérente car hors de phase : elle ne constitue qu’un « bruit ». Si l’on admet que la population des états d’énergie élevée est très faible dans les atomes en période de stabilité, il est facile de comprendre que pour stimuler l’excitation des électrons, il faut d’abord provoquer la formation d’une majorité d’éléments de haut niveau énergétique. En provoquant ensuite la stimulation par des micro-ondes (Masers) ou par la lumière (Lasers), il se produit une amplification considérable sous forme d’un faisceau puissant de rayonnement cohérent.

Les masers (Micro-wave Amplification by Stimulated Emission of Radiation) ont été réalisés les premiers par C.H. Townes et ses collaborateurs en 1955. Ils utilisent des méthodes de séparation des populations énergétiques quelque peu différentes de celle des lasers, par exemple au moyen de champs électriques ou magnétiques. Dans le laser à rubis, on agit directement sur les niveaux naturels des ions chrome dispersés dans la masse d’alumine : sous l’action de la décharge d’une puissante lampe-éclair, les ions chrome sont élevés à une large bande d’états excités puis tombent à un niveau métastable. De là se produit une chute vers l’état premier, toute l’énergie d’excitation se transformant en lumière de fluorescence rouge formée de deux raies étroites. La puissance de l’éclair électronique qui sert à élever le niveau énergétique des ions chrome est dite « puissance de pompage », et doit dépasser une certaine valeur. L’éclair étant court, l’émission de lumière amplifiée ne dure que 0,5 ms.
Pour éviter d’avoir à utiliser une grande puissance de pompage optique on préfère, comme élément amplificateur, la fluorine CaF2 contenant des ions Sm++ (samarium), et à la température de l’helium liquide : l’ion Sm »- possède en effet une forte raie d’émission dans le rouge avec une séparation des états initial et final mieux définie.
Les lasers à cristal ne sont pas à fonctionnement continu. Les systèmes continus nécessitent un milieu actif gazeux, par exemple du néon dans de l’hélium, soumis à des excitations électriques. L’hélium passe le premier à un état métastable et transmet son énergie d’excitation au néon, par collisions, par suite des faibles différences de niveaux de l’hélium métastable et du néon.

De nouveaux lasers à liquide organique (nitrobenzène) sont basés sur la stimulation de l’effet Raman dans lequel les vibrations moléculaires produisent une émission de longueur d’onde différente de celle de la lumière incidente. La stimulation doit cependant être amorcée à l’aide d’un laser à rubis.

Retrouvez moi sur Instagram